!image

ROOT Optimizer — A Balance of Speed and Stability in LLM Training

The core of ROOT lies in two major innovations: AdaNewton and soft-threshold denoising.

---

Background: Adam vs. Muon in LLM Optimization

Two prominent names in LLM optimization are Adam (including AdamW) and Muon:

• Adam/AdamW:
• A seasoned "goalkeeper" in deep learning, combining momentum and adaptive learning rates. Dominates training for many models but can suffer numerical instability in mixed-precision training for billion-scale parameters.
• Muon:
• A "game-changer" that treats weight matrices as coherent entities, reshaping training geometry via orthogonalization. However, its fixed coefficients and sensitivity to outlier noise reduce robustness.

The dilemma: For scaling models, must we choose between Adam’s stability and Muon’s speed?

Huawei Noah’s Ark Lab’s latest work — ROOT (Robust Orthogonalized OpTimizer) — offers an alternative.

ROOT corrects Muon’s accuracy issues across matrix dimensions and includes a gradient-noise “shock absorber” through soft-thresholding — targeting precision, stability, faster convergence, and resilience.

---

Research Context

• Paper: ROOT: Robust Orthogonalized Optimizer for Neural Network Training
• Link: https://arxiv.org/abs/2511.20626
• Repository: GitHub
• Authors: Wei He, Kai Han, Hang Zhou, Hanting Chen, Zhicheng Liu, Xinghao Chen, Yunhe Wang
• Institution: Huawei Noah’s Ark Laboratory

---

Evolution of Optimizers: From SGD to ROOT

In deep learning, the optimizer is the engine of training.

Early Stage: SGD

• SGD (Stochastic Gradient Descent): Updates parameters iteratively using gradients from mini-batches.
• Classical first-order method; struggles in complex loss landscapes without momentum.

Momentum and Adaptive Methods

• Momentum: Introduced to help effectively navigate valleys in the loss surface.
• Adam/AdamW: Combines momentum with per-parameter adaptive learning rates.
• Limitation: Treats parameters as scalars, ignoring intra-matrix correlations.

Matrix-Aware Optimization

• Muon: Orthogonalizes momentum matrices via Newton–Schulz iteration.
• Improves geometry normalization without added complexity (O(N)).
• Equivalent to steepest descent under spectral norm.
• Weaknesses:
• Fixed coefficients → dimension fragility.
• Sensitive to gradient outlier noise.

---

!image

ROOT Optimizer: Tackling Muon’s Weaknesses

ROOT uses two innovations to address Muon’s core limitations.

1. AdaNewton: Dimension-Specific Robustness

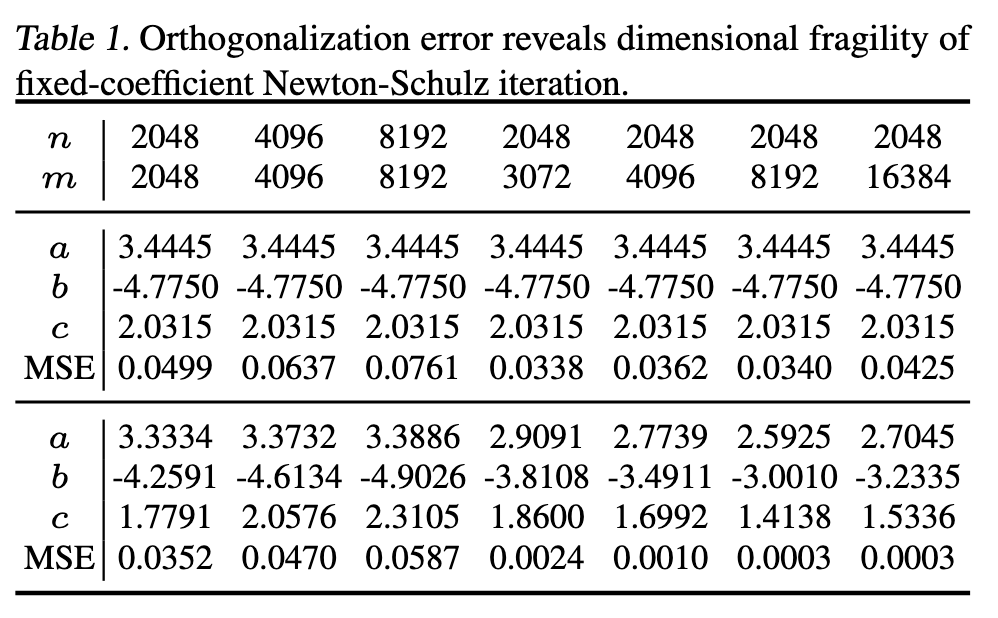
Problem: Fixed coefficients (a, b, c) in Muon’s Newton–Schulz iteration cause high orthogonalization errors for certain matrix shapes.

Solution:

• Adaptive Newton–Schulz Iteration (AdaNewton): Fine-grained coefficients tailored to each matrix dimension (m, n).
• Coefficients are derived from singular value distributions and can be jointly optimized during training.
• Ensures dimension-invariant orthogonalization precision.

---

2. Soft-Threshold Denoising: Filtering Outlier Gradients

Problem: Gradients display heavy-tailed distributions; outliers with extreme magnitudes disrupt orthogonalization.

Solution:

• Decompose gradient \(M_t\) into:
• Base component \(B_t\) — stable values.
• Abnormal component \(O_t\) — extreme values.
• Orthogonalize only \(B_t\); discard \(O_t\).
• Use soft-threshold operator (continuous alternative to hard clipping) to suppress extreme values while preserving relative magnitude rankings.

---

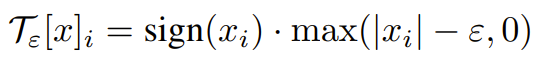
Experimental Validation

Huawei Noah’s Ark Lab tested ROOT on a 1B-parameter Transformer, across:

• Large-scale pre-training (on Ascend NPU clusters)
• Downstream LLM benchmarks
• Cross-modal tasks (computer vision)

Key Results

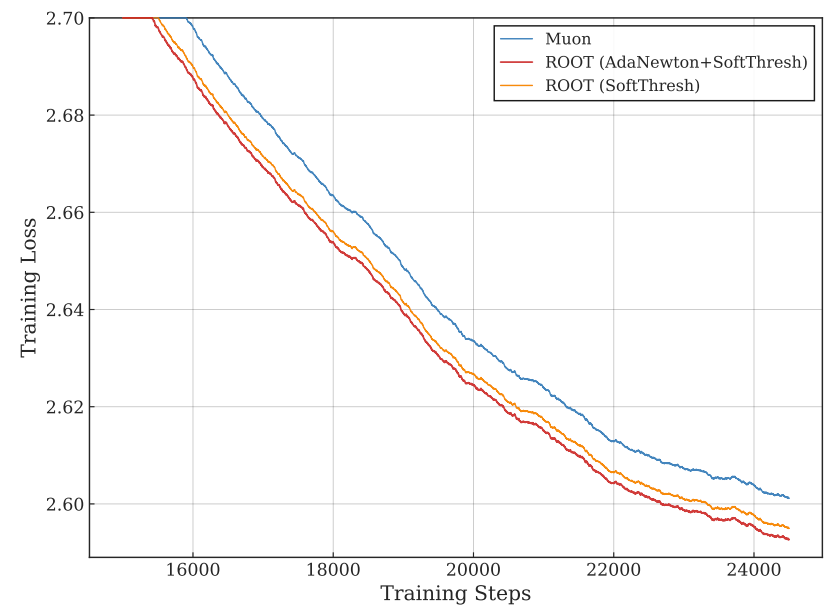
• Pre-training Loss:
• ROOT variants consistently outperformed Muon in a 10B-token run, achieving a final loss 0.01 lower.

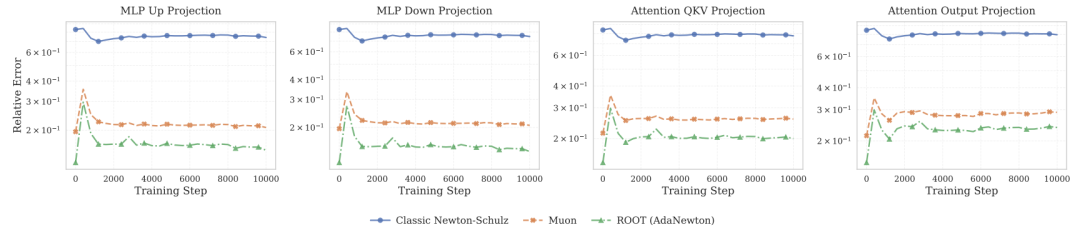
• Orthogonalization Accuracy:
• Adaptive coefficients kept precision close to true SVD across dimensions.

• Zero-shot Benchmarks:
• Average score: ROOT = 60.12, beating AdamW (59.05) and Muon (59.59).
• Led in 6 of 9 benchmarks.

• Cross-domain Generalization:
• On CIFAR-10 with ViT, ROOT + soft-threshold achieved Top-1 88.44%, surpassing Muon by ~4%.

---

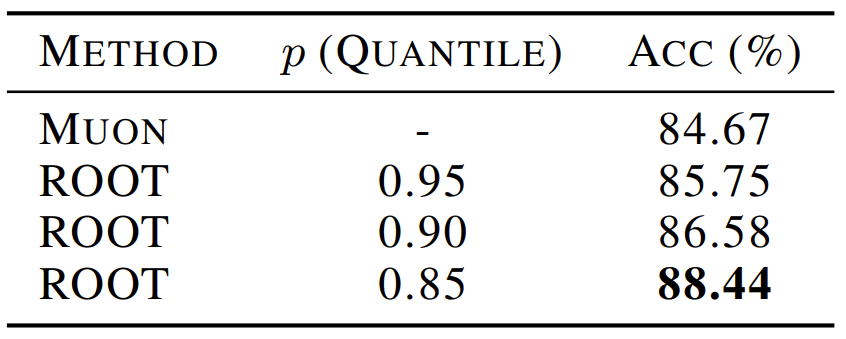
Implications: A New Era of Optimizers?

ROOT marries matrix-aware speed with scalar-method stability — resolving Muon’s issues without sacrificing efficiency.

Key Takeaways:

• AdaNewton eliminates dimension fragility.
• Soft-threshold denoising tackles heavy-tailed gradient noise.
• ROOT is cross-domain capable (LLM + CV).
• Open-source code accelerates adoption in trillion-parameter training.

---

Team Spotlight

Kai Han — Co-first Author

• Senior researcher, Huawei Noah’s Ark Lab
• PhD: Institute of Software, Chinese Academy of Sciences
• 50+ AI papers, 21,000+ citations
• Author of GhostNet, TNT
• Area Chair for NeurIPS, ICML, ICLR, CVPR, ICCV, AAAI, ACMMM

Wang Yunhe — Corresponding Author

• Director, Huawei Noah’s Ark Laboratory
• Focus: AI foundation models and optimization research.

---

Related Platform: AiToEarn

Platforms like AiToEarn官网 bring research innovations into content ecosystems:

• AI-based content generation
• Multi-platform publishing (Douyin, Kwai, WeChat, Bilibili, Rednote, Facebook, Instagram, LinkedIn, Threads, YouTube, Pinterest, X/Twitter)
• Analytics & model ranking (AI模型排名)
• Supports creators in monetizing AI-generated content at scale.

---

Read Original

Open in WeChat