Large Model Intelligence｜4-Bit Quantization Frontier

Introduction: Balancing Compression and Accuracy

In our previous discussion on 8-bit quantization (W8A8), pioneers balanced accuracy with efficiency, pointing the way toward slimmer and faster large models.

But for enormous models—with parameters in the hundreds of billions to trillions—8-bit remains too large to fit into mainstream hardware.

• Example:
• A 70B model at 8-bit still takes ~70 GB. This exceeds most consumer GPUs’ VRAM and even many enterprise inference cards, making deployment impractical.

Goal:

Break the “VRAM wall” so powerful LLMs can run locally for mass accessibility.

Solution path: Push compression further into 4-bit quantization.

---

Why 4-Bit Quantization Is Hard

> Moving from 8-bit (256 values) to 4-bit (16 values) is like replacing a precision caliper with a basic ruler for measuring micromechanical parts.

Challenges:

• Quantization error is amplified
• Naïve methods cause catastrophic accuracy loss

Opportunities:

A new generation of algorithms tackle these issues with ingenuity:

• GPTQ – Layer-wise reconstruction with error compensation
• AWQ – Protects key weights based on activation importance
• QLoRA – Combines 4-bit quantization with LoRA fine-tuning
• FlatQuant – Learns optimal layer-wise transformations for full W4A4

---

01 – GPTQ: Precision Sculpting with Error Compensation

Core Idea: Layer-Wise Non-Destructive Reconstruction

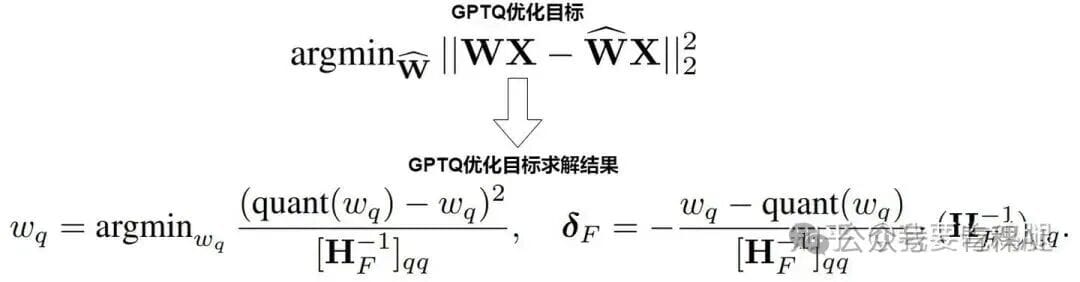
Instead of sidestepping complexity, GPTQ treats quantization as a problem of finding a quantized weight matrix that keeps the Mean Squared Error (MSE) of the layer’s output minimal.

Formula:

\[

\min_{W_q} \; \| f(W_q, X) - f(W, X) \|_2^2

\]

Strategy:

• Quantize one weight at a time.
• Immediately adjust remaining unquantized weights using inverse Hessian-based sensitivity measures.
• Repeat until all weights are quantized.

---

Theoretical Roots: OBD → OBS → OBQ

OBD (Optimal Brain Damage)

• Purpose: Select weights to prune without large loss increase
• Approach: Second-order Taylor approximation; assumes independent weights.

OBS (Optimal Brain Surgeon)

• Purpose: Improve upon OBD
• Approach: Use full Hessian; prune one weight and compensate others immediately.
• Drawback: Requires costly inverse Hessian (O(N³) complexity).

OBQ (Optimal Brain Quantization)

• Insight: Pruning is a special case of quantization.
• Approach: Quantize one weight, compensate others via inverse Hessian correlation.

---

GPTQ’s Three Innovations

To make OBQ efficient for large models, GPTQ introduces:

• Fixed Quantization Order –
• Enables full parallelization by quantizing columns in a fixed sequence.
• Lazy Batch-Update –
• Delays compensation until blocks of columns are processed, reducing I/O overhead.
• Cholesky Decomposition –
• Avoids precision drift by replacing explicit inversion with stable triangular solves.

---

GPTQ Summary

Pros:

• Near-lossless accuracy at 4-bit
• Applicable to most Transformer models

Cons:

• Still time-consuming offline process
• Accuracy depends heavily on calibration dataset quality

---

02 – AWQ: Activation-Aware “Key Protection”

Observation: Not All Weights Are Equal

AWQ focuses on critical minority weights—those in high-activation channels.

Evidence:

Protecting just 1% of such weights at higher precision nearly restores baseline model accuracy.

---

Approach: Scaling Significant Weights

• Step 1: Identify channels with largest average activations from calibration data.
• Step 2: Pre-amplify weights in these channels by scale factor \(s>1\) before quantization.
• Step 3: During runtime, divide corresponding activations by \(s\) (fused to earlier ops) for mathematical equivalence with no overhead.

---

Finding Optimal Scaling

• Reduce search to a single scalar factor \(\alpha\in[0,1]\).
• Perform quick grid search to minimize quantization error.

---

AWQ Summary

Pros:

• Simple, fast, hardware-friendly
• Accuracy rivaling GPTQ in many cases

Cons:

• Assumes minority weight protection suffices
• Depends on representative calibration dataset

---

03 – QLoRA: Quantization + Low-Rank Fine-Tuning

Problem: Fine-Tuning Large Models Is Expensive

Standard LoRA requires base model in FP16. QLoRA enables fine-tuning quantized 4-bit bases.

---

Core Idea: “Greenhouse on Ice”

• Frozen ice layer: Static 4-bit NF4 quantized base model
• Greenhouse: Tiny BF16 LoRA adapters trained on top

---

Three Innovations:

• NF4 Data Type: Optimal for normal-distributed weights; uses quantile points.
• Double Quantization: Further compress per-block scaling factors from FP32 to 8-bit.
• Paged Optimizers: Dynamic VRAM management to absorb memory spikes.

---

QLoRA Summary

Pros:

• Fine-tune up to 65B models on 24 GB GPU
• Dramatically lowers hardware barrier

Cons:

• No inference speedup/memory benefit—only training

---

04 – FlatQuant: Learned Optimal Transformations

Goal: Full W4A4 Quantization

Flatten both weights and activations for consistent quantization.

---

Issues with Existing Transforms

• Per-channel scaling: Limited channel-to-channel transfer
• Hadamard transform: Same orthogonal transform for all layers, mismatched difficulties

---

Solution: Learn Layer-Specific Affine Transformation

• Matrix P: Optimized per layer with calibration data to flatten distributions
• Kronecker Decomposition: Factor P into small matrices to cut parameters and compute cost.

---

FlatQuant Summary

Pros:

• Top accuracy for full 4-bit W4A4 quantization
• Layer-specific transformation

Cons:

• More complex and requires learning step

---

Closing Thoughts

4-bit quantization is crucial for accessible deployment of large models.

Each algorithm offers unique trade-offs:

• GPTQ: Mathematical optimality, slower offline
• AWQ: Fast, intuitive heuristic
• QLoRA: Enables efficient fine-tuning of quantized models
• FlatQuant: Learns layer-specific smoothing for hardest scenarios

Choosing the right method depends on:

• Accuracy needs
• Available calibration data
• Target tasks: inference acceleration vs fine-tuning

---

Tip for Practitioners:

Pair your model optimization workflow with streamlined publishing and monetization tools to maximize real-world impact—e.g., integration with platforms that handle generation + multi‑channel deployment + analytics for AI-powered content. This ensures your technical advances reach and benefit users quickly.