In Math, Chinese Models Never Lose: DeepSeek Dominates Overnight, Math V2 Ends the 'Strongest Math Model' Debate

DeepSeek-Math V2: Self-Verifiable Mathematical Reasoning Breakthrough

On November 27, without prior announcement, DeepSeek open-sourced its new mathematical reasoning model DeepSeek‑Math V2 (685B parameters) on Hugging Face and GitHub.
> Key milestone: First openly available math model to achieve International Mathematical Olympiad (IMO) gold medal level.
---
Background & Progress

- Previous version: DeepSeek-Math‑7B
- Released over a year ago
- ~7B parameters
- Performance comparable to GPT‑4 and Gemini‑Ultra
---
Performance vs Benchmarks
IMO‑ProofBench Results
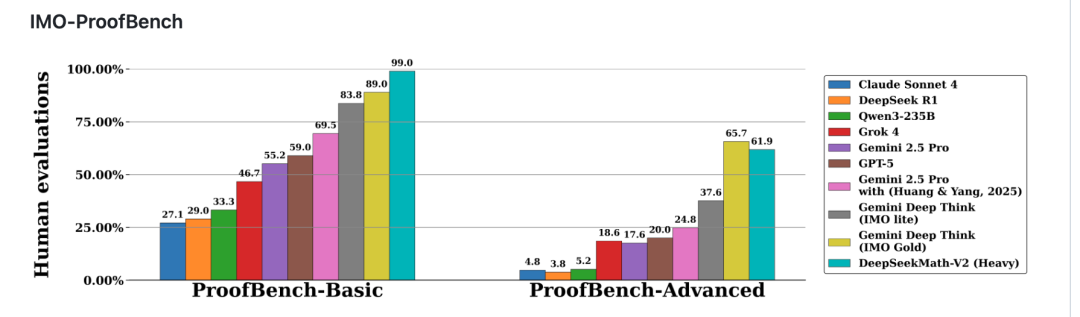
- Basic subset:
- Math‑V2: ≈99%
- Gemini DeepThink (IMO Gold): 89%
- Advanced subset:
- Math‑V2: 61.9%
- Gemini DeepThink: 65.7%
---
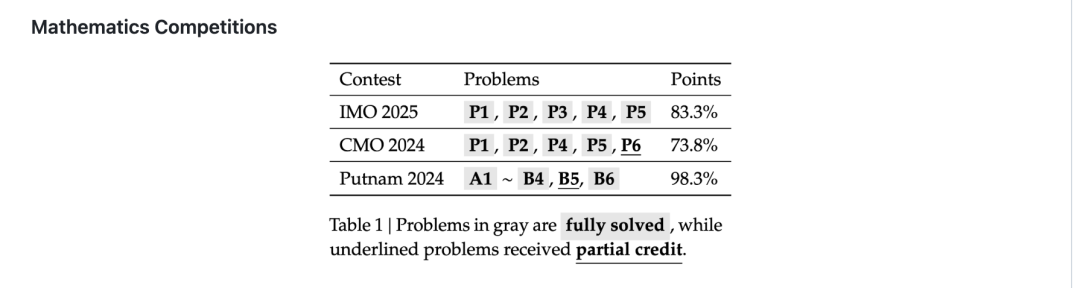
Real Competition Achievements
- IMO 2025: Gold medal standard achieved
- CMO 2024: Gold medal level performance
- Putnam 2024: Scored 118/120 in extended evaluation
- Strong theorem-proving abilities without large “answer banks” in training
---
The Research Paper
DeepSeek Math‑V2: Towards Self‑Verifiable Mathematical Reasoning

Key Findings
- Reinforcement learning using final answer correctness improves competition scoring but has limitations:
- Correct answer ≠ Correct reasoning
- Open problems have no standard answers — purely result‑based rewards are ineffective
- Self‑verification is essential to:
- Validate reasoning chains
- Improve reliability
- Handle open-ended proofs
---
Why Self‑Verification Matters
Mathematics demands rigor — a single logical gap invalidates the conclusion.
Self‑verification enables models to:
- Check completeness & logical consistency
- Refine reasoning multiple times before finalizing
- Continue improving without human labels for open problems
- Avoid “right answer, wrong process” issues
---
DeepSeek’s Self‑Verification Approach
Development Shift: From result-oriented to process-oriented.
Implementation Steps:
- Train a high‑precision validator to check proof correctness
- Use validator as reward model to guide the proof generator
- Enable model to detect and fix flaws before submitting final proof
- Introduce expanded verification capacity — automatically label hard‑to‑verify reasoning samples
- Iteratively train both validator and generator in a feedback loop
Impact:
- Helps tackle open problems without standard solutions
- Moves AI from “solving problems” toward “thinking like a mathematician”
---
Community Reactions
Overseas Developer Communities
> “The DeepSeek whale has finally come back.” — Reddit user
Highlights:
- Surprise at beating Gemini DeepThink Basic benchmark by +10%
- Anticipation for future DeepSeek programming model
- Recognition of mathematics as essential for AI advancement
- Interest in applying math reasoning strength to code generation
X (Twitter)
- Recall of V1 being released nearly 2 years ago
- Praise for continuous behind‑the‑scenes development leading to major performance gains

Zhihu (China)
> “Mathematical reasoning is the most demanding of all AI tasks… a single error collapses the whole argument.”

---
Strategic Implications
With DeepSeek‑Math V2 open‑sourced:
- The competitive landscape for math reasoning AI is evolving
- Self‑verifiable reasoning is emerging as a key path for next‑gen AI systems
---
Related Ecosystem: AI Content Monetization
Platforms like AiToEarn demonstrate how iterative validation and multi‑platform publishing can extend AI output value.
Features:
- Generate, publish, and monetize AI content across Douyin, Kwai, WeChat, Bilibili, Xiaohongshu, Facebook, Instagram, LinkedIn, Threads, YouTube, Pinterest, and X
- Connects generation tools, publishing, analytics, and model ranking
- Ensures quality and reach — mirroring Math‑V2’s self‑verification ethos
---
DeepSeek-Math V2 Summary
Core strengths:
- Improved accuracy across symbolic reasoning, algebra, and advanced math
- Optimized multi‑step logic
- Expanded dataset for broader domain coverage
- Faster response times
- Integrable with educational, research, and proof‑checking systems
---
Ideal Use Cases
- STEM Education: Step‑by‑step learning assistance
- Academic Research: Proof verification and theorem exploration
- Code Generation: Especially for math‑heavy applications
- Automated Proof Systems: Formal verification/model checking
---
Reference: GitHub Repo | Paper PDF
---
Bottom line:
DeepSeek-Math V2’s self‑verification mechanism reflects a paradigm shift — from maximizing correct answers to ensuring correct reasoning. This positions it not just as a competition-winning model, but as a genuine research partner in mathematics and beyond.



