Post-90s Chinese Associate Professor Solves 30-Year-Old Math Conjecture — Directly Linked to Generative AI

Breakthrough: Talagrand Convolution Conjecture Solved
A 30-year-old mathematical puzzle — the Talagrand Convolution Conjecture — has finally been solved by Yuansi Chen, a young Chinese mathematician born in the 1990s.
Chen, from ETH Zurich, recently published his result on arXiv:

His paper proves the conjecture for the Boolean hypercube, accurate up to a log log η factor.
This breakthrough is noteworthy because it establishes a rigorous mathematical foundation for smoothing techniques in high-dimensional discrete spaces, with direct implications for machine learning.
ML-Relevant Contributions
- Regularization theory support — better understanding of how convolution smooths functions.
- Concrete mathematical tools for building generative AI models that work with discrete data.
The conjecture was originally posed in 1989 by Michel Talagrand, Abel Prize laureate (often called the “Nobel of Mathematics”).
---
Core Ideas Behind the Conjecture
1. Heat Smoothing
Imagine a massive high-dimensional "chessboard" where each cell has a binary state. A function defined on this space can have sharp peaks and valleys.
Using convolution or heat semigroup operations is like "heating" the space:
- Heat diffuses.
- Large values flow into nearby smaller values.
- Peaks flatten and valleys rise.
2. Markov’s Inequality
Markov’s inequality states that for a non-negative random variable:
> If the mean is 1, the probability of exceeding 100 (η) is at most 1%.
Formally, it’s bounded by `1/η`.
Talagrand’s insight: After heat smoothing in specific probability spaces (Gaussian or Boolean hypercube), the probability of extreme values should be far lower than Markov’s bound.
He predicted this reduction involves an extra factor related to:

In simple terms, smoothed data are even less likely to produce extreme outliers — and this probability can be quantified.

AI-generated illustration
---
Why the Discrete Case Was Hard
While the Gaussian (continuous) version of the conjecture had been solved, the discrete Boolean hypercube remained unsolved due to:
- Lack of calculus-based smoothness tools.
- Inapplicability of stochastic differential equations.
Chen’s Approach
- Adapted Gaussian-space stochastic analysis to discrete systems.
- Leveraged properties of the reverse heat process.
- Designed state-dependent perturbations for the Boolean hypercube — δ varies with state and coordinates.
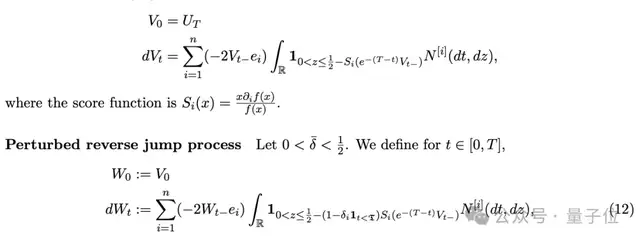
Final result:
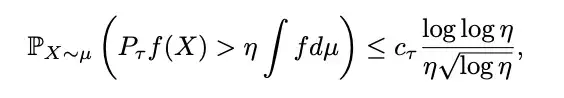
Chen resolved the conjecture up to a negligible log log η factor, effectively providing a full solution.
---
Implications for ML & Generative AI
Although the work is pure probability theory, it strongly aligns with ML principles:
- Reverse heat process parallels diffusion models — useful for generative models with discrete data.
- Offers a quantitative measure of convolution’s regularization effect.
- Explains why adding noise/smoothing stabilizes models in complex high-dimensional spaces.
Because much ML data is high-dimensional and discrete, this adds valuable geometric understanding for learning theory, binary datasets, and logical functions.
---
About Yuansi Chen

- Born July 1990, Ningbo, Zhejiang, China.
- Research in statistical machine learning, Markov chain Monte Carlo, applied probability, and high-dimensional geometry.
- Ph.D. — University of California, Berkeley (2019), supervised by Bin Yu.
- Postdoc — ETH Zurich (2 years).
- Assistant Professor — Duke University (2021–2024).
- Associate Professor — ETH Zurich (2024–present).
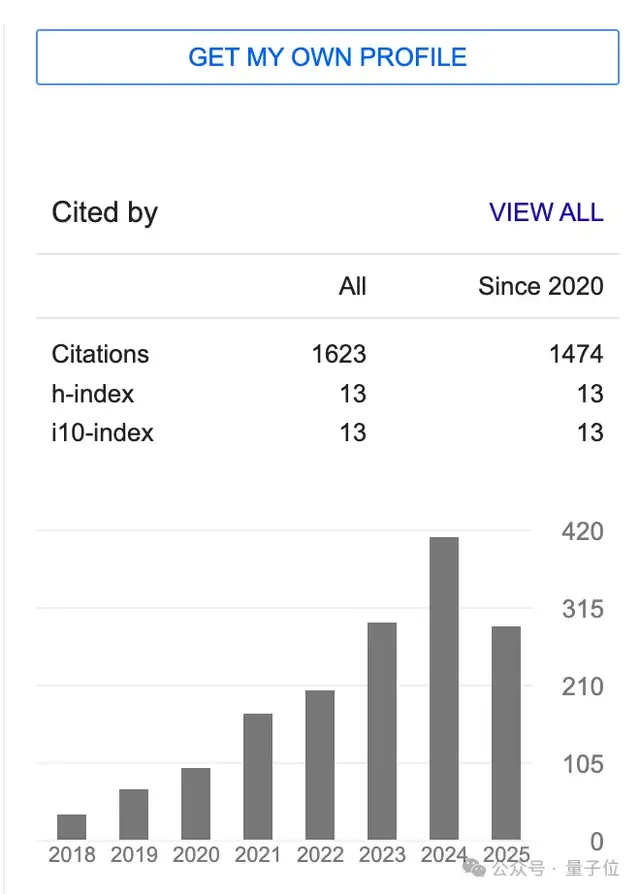
- Google Scholar: 1,623 citations, h-index 13.
Awards:
- 2023 Sloan Research Fellowship.
His earlier work solved the KLS conjecture (“apple-cutting problem”) — a famous 25-year unsolved problem in mathematics.
---
Paper Link
https://arxiv.org/abs/2511.19374
---
AiToEarn: From Theory to Reach
Platforms like AiToEarn help transform research breakthroughs into distributed, monetizable content.
Key capabilities:
- AI-assisted content generation.
- Cross-platform publishing.
- Analytics and AI model rankings.
Publishing channels include: Douyin, Kwai, WeChat, Bilibili, Xiaohongshu, Facebook, Instagram, LinkedIn, Threads, YouTube, Pinterest, X/Twitter.
Learn more via the AiToEarn Blog or explore the GitHub repository.
---
Summary: Yuansi Chen’s result not only closes a decades-old conjecture but also bridges deep mathematics with emerging ML applications, particularly in generative AI for discrete spaces. The methods may inspire future learning algorithms grounded in rigorous probability theory.



