Scaling Laws and Best Practices for Large Model RL

2025-10-30 · Jiangsu
The paper The Art of Scaling Reinforcement Learning Compute for LLMs from Meta proposes a scaling law for RL applied to LLMs, performs extensive comparisons and ablations, and distills these insights into what may be considered the current best RL recipe.
---


Why This Paper Matters
This work effectively consolidates years of RLHF-related innovations for LLMs into one clearly written reference. It blends theoretical scaling insights with empirical design guidelines, providing actionable recipes for practitioners.

---
Abstract Summary
Reinforcement Learning is now a core component in LLM training. While pre-training benefits from well-understood scaling laws, RL has lacked such a guide.
Key contributions:
- Identified the scaling law for LLM RL through 400,000 GPU-hours of experiments.
- Used this scaling law to evaluate various RL designs, culminating in a best-practice RL recipe.
---
RL Scaling Law
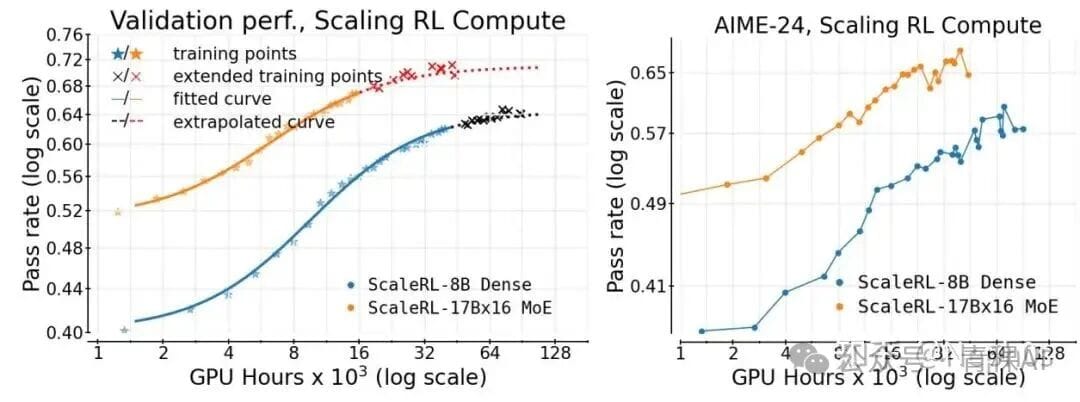
Experimental setup:
- 50,000 GPU-hours on
- 8B dense model
- 17B × 16 MoE model
- Measured i.i.d validation performance over ~7000 steps.
Findings:
- Performance fits a sigmoid-shaped scaling curve.
- Extrapolations align with extended training results — proving predictive validity.
- Downstream evals (AIME-24) follow the same curve.
Formula:

> RL Improvement = A × f(C)
> where f is a sigmoid over compute investment C.
Curve parameters:
- A (Upper Limit) — max converged performance.
- B (Learning Efficiency) — efficiency factor.
- C_mid — compute needed to reach half of possible improvement.
---
---
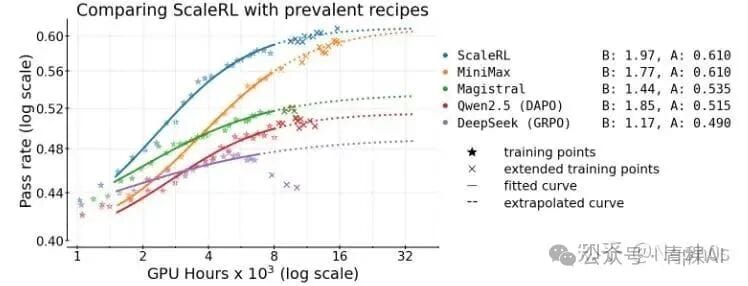
Empirical RL Design Studies
Asynchronous RL Setups
Variants:
- PPO-off-policy-k
- Used in Qwen3, ProRL. Generate B prompts, split into k minibatches (B/^). Gradient updates on minibatches; older policy used for rollouts.
- Pipeline-RL-k
- Used in Magistral. Trainer updates instantly loaded into generator; generator continues pre-generated tokens using new params. Parameter k limits how far trainer is ahead.
Background:
Generation/training often run in different frameworks — LLM models in each can have independent parameters and implementations.
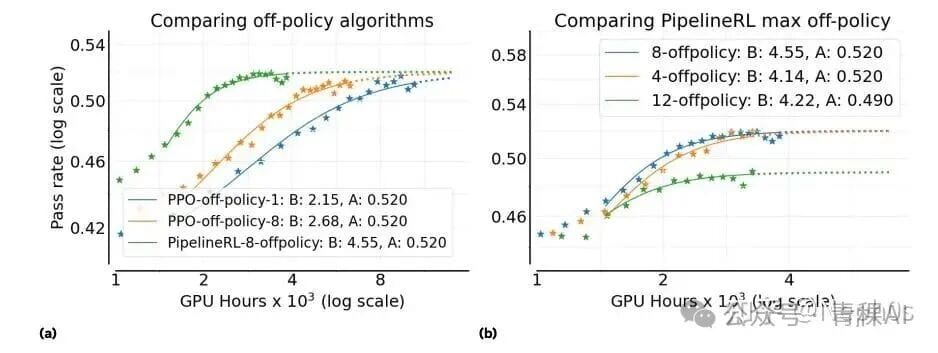
Conclusions:
- Pipeline RL and PPO-off-policy share same A.
- Pipeline RL has higher B (efficiency).
- Optimal k = 8.
---
Loss Function Variants
Common Methods:
- DAPO — Token-level clipping; clipped tokens not contributing gradients.
- GSPO — Sequence-level clipping.
- CISPO — Vanilla REINFORCE base; clipping + stop-gradient during importance sampling; clipped tokens still influence gradients.
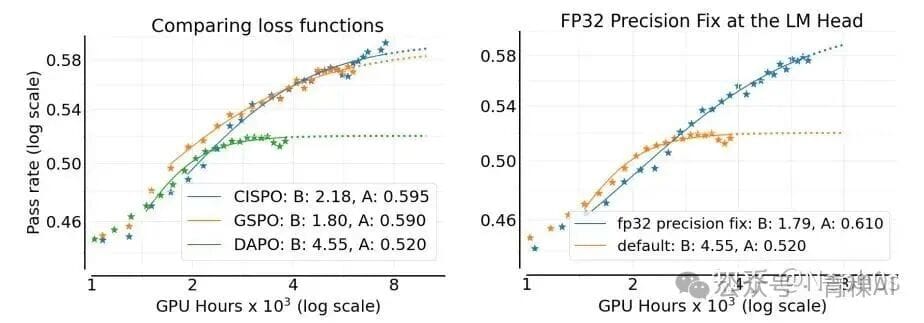
Conclusions:
- CISPO > GSPO > DAPO in A (performance ceiling).
---
FP32 Precision for Logits
Conclusion:
Using FP32 for logits in both generator and trainer leads to significant gains. (Minimax-M1 proposal)
---
Loss Aggregation Strategies
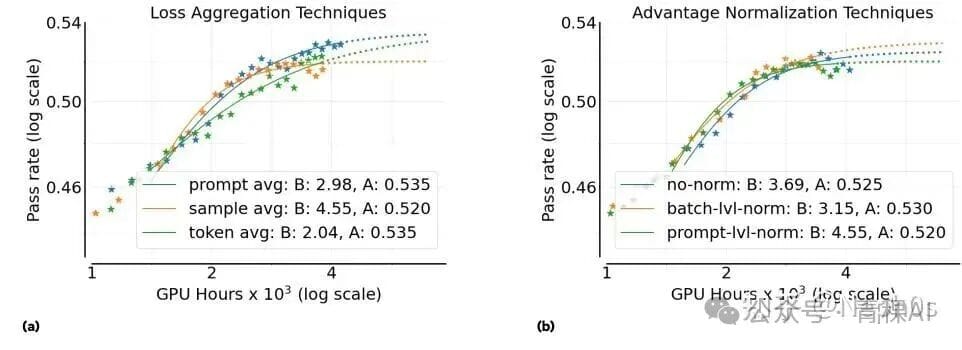
Options:
- Sample Averaging — per trajectory (GRPO).
- Prompt Averaging — per prompt (DAPO).
- Token Averaging — across the batch.
Conclusion:
Prompt averaging performs best.
---
Advantage Normalization
Methods differ in Std computation:
- Std over rollouts per prompt (GRPO).
- Std over batch.
- No Std (Dr.GRPO).
Conclusion:
All perform similarly; method (2) preferred on theoretical grounds.
---
Zero-Variance Filtering
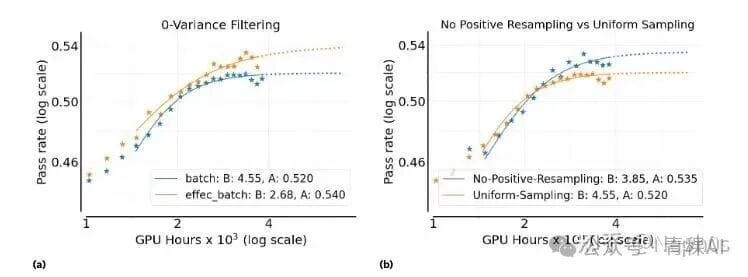
Idea: Remove prompts with identical rewards across rollouts.
Result: Improves performance.
---
Adaptive Prompt Filtering
- Strategy: Remove prompts with >0.9 average accuracy (Polaris).
- Result: Increases A.
---
Recommended RL Recipe — ScaleRL
From findings, the optimal recipe includes:
- PipelineRL (k=8)
- Interruption-based length control
- FP32 logits
- CISPO loss
- Prompt-level loss aggregation
- Zero-variance filtering
- No-positive resampling
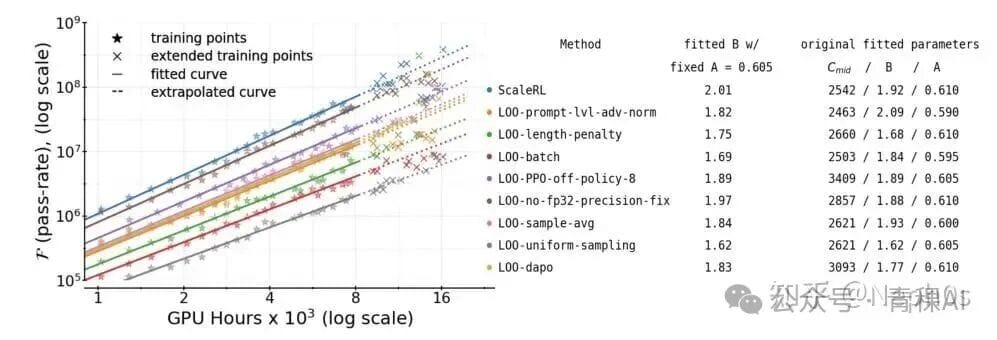
Ablation confirms each component’s contribution.
---
Factors Affecting RL Scaling
Model Size
Scaling law applies to 7B and 17B×16 MoE models.
Context Length
Longer contexts reduce B but raise A.
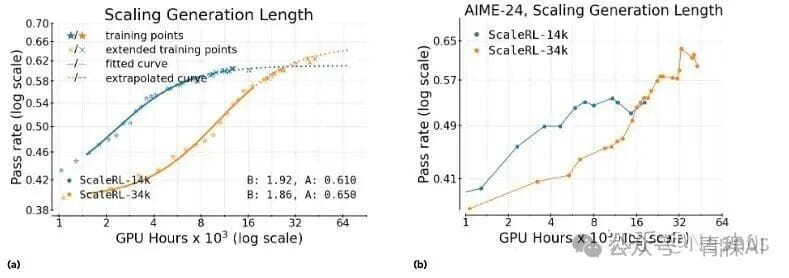
Batch Size
Small batches help early performance; large batches raise final A when compute is abundant.
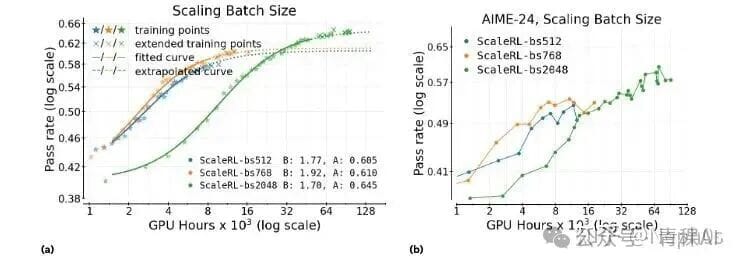
Rollout Number
With fixed batch size, varying n_rollout and n_prompt has no effect on training.
---
Takeaways

Scaling Law:
- Performance curve is sigmoid in log-compute space.
- A and B depend on model, algorithm, and design choices.
Principles:
- Algorithm design sets RL’s upper bound — not a universal constant.
- Small-scale wins may not scale; estimate A/B before committing huge compute.
- Many designs alter B but not A (loss aggregation, curriculum learning, length penalties, adv norm).
ScaleRL offers a tested optimal RLHF recipe for modern LLMs.
---
Community & Resources
Join AINLP Tech Group:
WeChat: ainlp2 (Include your focus area in the request.)

About AINLP:
Community for AI, ML, DL, NLP — from LLMs, text generation, chatbots, MT, KG, recommendation, ads, to shared job info and experiences.

---
Practical Deployment Tip:
For labs and creators, scaling training insights into deployed AI systems benefits from integrated workflows.
Platforms like AiToEarn官网 package AI generation, publishing, analytics, and monetization — allowing direct syndication to Douyin, Kwai, Bilibili, Xiaohongshu, FB, IG, Threads, YouTube, Pinterest, X/Twitter — aligning the efficiency principles from RL scaling with global content reach.
---



