# Terence Tao’s Latest Reflections on AI in Mathematical Research

Renowned mathematician **Terence Tao**, a Fields Medal laureate, is not only pushing boundaries in mathematics but also **actively experimenting with AI collaboration**—exploring its potential in solving complex mathematical problems.
Recently, Tao used **ChatGPT‑5 Pro** to tackle an open problem unknown to him: the *sphere with bounded curvature*. His work provides fascinating insights into **AI’s strengths and limitations** in mathematical research.
---
## Key Insights from Tao’s Experiment
Tao observed that AI’s usefulness varies significantly depending on the level of scale:
- **Micro Scale** (concrete derivations & computations): **Extremely useful**
- **Medium Scale** (strategy selection & direction finding): **Limited help, sometimes distracting**
- **Macro Scale** (understanding problem structure & key difficulties): **Regains value**
> “To evaluate a tool’s value, one must measure it across multiple dimensions.”

---
## The “Sphere with Bounded Curvature” Problem
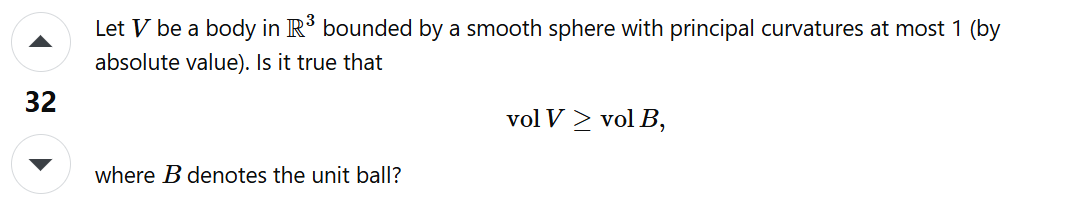
**Mathematical Statement**:
In three‑dimensional Euclidean space \( \mathbb{R}^3 \), if a smooth immersed sphere has both principal curvatures within absolute value ≤ 1, is its enclosed volume **at least** that of the unit sphere?
### Approach
Tao viewed it as a **variational problem** with two regimes:
1. **Perturbative regime**: sphere close to the standard sphere
2. **Non‑perturbative regime**: sphere far from the standard sphere
Due to limited geometric intuition and tools favoring the perturbative case, Tao focused on **non‑perturbative analysis**.
---
## Shift to the Star‑Shaped Case
Tao expanded his scope after comments suggesting the convex case was too simple.
### Hypothesis
- Express problem constraints and conclusions in **integral form** over the surface
- Advance via **integral inequalities**
Because his differential geometry knowledge was rusty, Tao asked AI to perform the calculations.
**Surprising Result:**
AI computed all quantities accurately and produced a **complete proof** for the star‑shaped case using:
- **Stokes’ theorem**
- **Willmore inequality**
- **Gauss–Bonnet theorem**
- **Minkowski first integral formula** (new to Tao)
With these, AI reduced the proof to **one line of derivation**.
---
## Verification and Additional Proofs
Tao manually verified each step:
- **Reference gap** found: Minkowski formula often stated without full proof
- **AI’s response**: Provided two convincing proofs:
1. Based on the **divergence theorem** (aligned with Tao’s idea)
2. Using a **flow method** Tao hadn’t considered
---
## AI Performance in the “Almost Round” Case
Tao explored the case where mean curvature ≈ 1, treating it as a **perturbative elliptic PDE** problem.
**AI’s contribution:**
- Applied coercive elliptic estimates to show the theorem holds when mean curvature is close to 1
- Noted that this assumption **implies star‑shapedness**
- Minor error: Slight miscalculation of a perturbed nonlinear term
---
## Discovery of Limits in AI Strategy Guidance
When Tao’s numerical brute‑force idea was discussed, AI agreed but did not critique flaws in the assumption—example of **over‑agreement behavior**.
**Medium‑scale takeaway:**
AI may **reinforce incorrect intuition** instead of challenging it.
---
## Critical Realization About the Problem’s Difficulty
Through further reading, Tao discovered:
- The real challenge involves **extremely non‑round geometries**
- Examples: long thin tubes, slender cylinders, flat sheets
- Star‑shaped case is one of the easier scenarios (seen in Pankrashkin’s and Qiu’s work)
- The problem remains **open** and beyond Tao’s current toolkit
---
## Role of AI in Tao’s Research Process
**Strengths:**
- Expanded Tao’s mathematical toolkit
- Suggested methods outside his habitual approach
- Accelerated proof verification
**Weaknesses:**
- Lacked strategic criticism
- Occasionally amplified incorrect assumptions
**Macro insight:**
AI can help explore, test, and discard unsuitable ideas faster, and introduce unfamiliar concepts.
---
## Platforms for AI‑Assisted Research Publishing
Tao’s experience shows value in structured AI integration.
Open‑source platforms like [AiToEarn官网](https://aitoearn.ai/) enable:
- **AI content generation**
- **Multi‑platform publishing** (Douyin, Kwai, WeChat, Bilibili, Rednote, Facebook, Instagram, LinkedIn, Threads, YouTube, Pinterest, X)
- **Analytics & model ranking** ([AI模型排名](https://rank.aitoearn.ai))
Useful for:
- Documenting research
- Disseminating work to diverse audiences
- Monetizing insights
---
## Final Thoughts from Tao
Comparing with a prior AI experiment:
- If researcher **already has strong intuition**, AI’s role is verification
- If **no clear intuition**, AI’s output may be creative but **harder to trust and guide**
**Takeaway:** Collaborating with AI in unfamiliar fields has **exploratory value**, but requires vigilance to avoid plausible‑yet‑misleading results.
---
**Reference:** [https://mathstodon.xyz/@tao](https://mathstodon.xyz/@tao)

---
For broader AI‑driven creation & research, [AiToEarn官网](https://aitoearn.ai/) offers an ecosystem to:
- Generate content with AI
- Distribute across channels
- Track performance and earnings
Ensuring both **creative exploration** and **practical impact**.
[Read the original](2650994886)
[Open in WeChat](https://wechat2rss.bestblogs.dev/link-proxy/?k=f8727651&r=1&u=https%3A%2F%2Fmp.weixin.qq.com%2Fs%3F__biz%3DMzA3MzI4MjgzMw%3D%3D%26mid%3D2650994886%26idx%3D2%26sn%3Df466263ac3a038b524076a4afa569a37)




