The Forgotten Solution to a Human Problem, Rediscovered by GPT-5
Rediscovering a Lost Solution with GPT‑5 Pro
This case revolves around Erdős Problem #339, one of nearly a thousand problems posed or relayed by the famed mathematician Paul Erdős, archived at erdosproblems.com.
The site tracks each problem’s status:
- About one‑third have been solved.
- Most remain open, serving as long‑term challenges for the mathematical community.
Previously: Erdős Problem #339 was marked unsolved, classified among significant open problems, and continued to attract researcher interest.
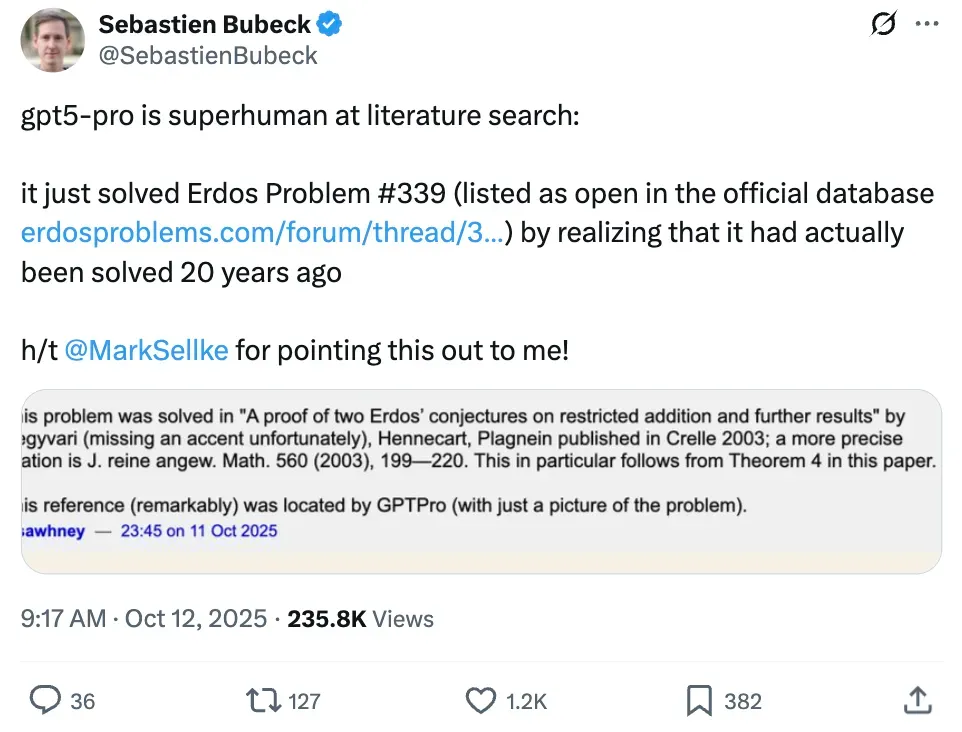
Recently: A user running GPT‑5 Pro discovered that the problem was already solved back in 2003 — a breakthrough in “knowledge archaeology” made possible from an image alone.
---
AI Finds the Forgotten Proof
Remarkably, GPT‑5 Pro identified the key paper by reading only a screenshot of Erdős Problem #339.
OpenAI researcher Sebastien Bubeck shared the finding online, sparking wide discussion.
> Incidentally, Terence Tao used ergodic theory tools to solve another famous Erdős challenge — the “Erdős discrepancy problem,” which had stumped mathematicians for decades.
---
Erdős Problem #339 — Statement
The problem is a classic in additive number theory:
> Let \( A \subseteq \mathbb{N} \) be an additive basis of order \( r \) (i.e., every sufficiently large integer can be expressed as the sum of \( r \) elements of \( A \)). Is it true that the set of integers expressible as the sum of exactly \( r \) distinct elements of \( A \) always has positive lower density?
A related question posed by Erdős and Ronald Graham:
- If integers expressible as the sum of \( r \) elements of \( A \) have positive upper density, does the same hold for integers expressible as exactly \( r \) distinct elements?

---
Pre‑Discovery Discussions
Before GPT‑5 Pro’s find, discussions on the problem’s page explored:
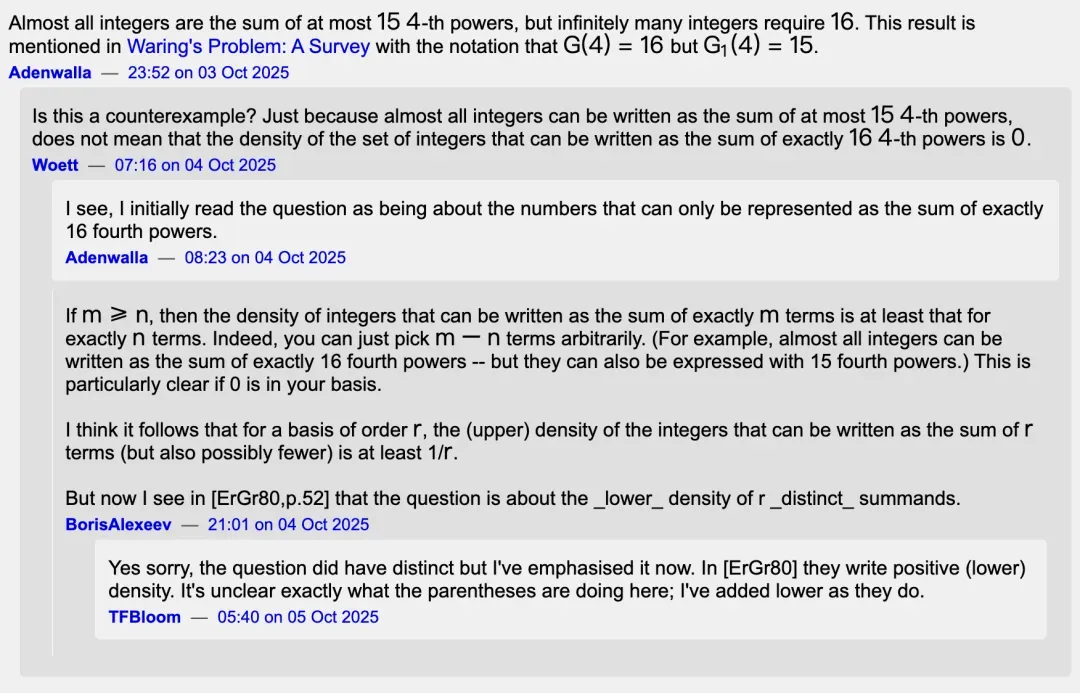
- Connections to Waring’s Problem:
- User Adenwalla noted:
- Almost all integers can be expressed as ≤15 fourth powers.
- Some require exactly 16 terms → \( G(4) = 16 \), \( G_1(4) = 15 \).
- Raised speculation: Could such results mean the additive basis question’s lower‑density property might fail?
- Counterexample invalidation:
- Woett and BorisAlexeev pointed out Waring’s problem allows repeats.
- Erdős Problem #339 requires distinct summands — stricter conditions.
---
Deepening the Debate
Further exchanges included:
- Zach Hunter: Studied density stability at large scales.
- Woett: Proposed set constructions as counterexamples.
Core discussion points:
- “Distinct elements”
- “Lower density”
- “Bounded doubling”
Outcome: No construction successfully drove lower density to zero for exactly \( r \) distinct elements.

---
The Revelation — Proof from 2003
Eventually, msawhney reminded everyone: This problem was resolved in 2003.
Reference:
Hegyvari, Hennecart, Plagne — “A proof of two Erdos’ conjectures on restricted addition and further results”, J. reine angew. Math. (Crelle), Vol. 560, pp. 199–220.

Key: Theorem 4 of the paper directly solves Erdős Problem #339.
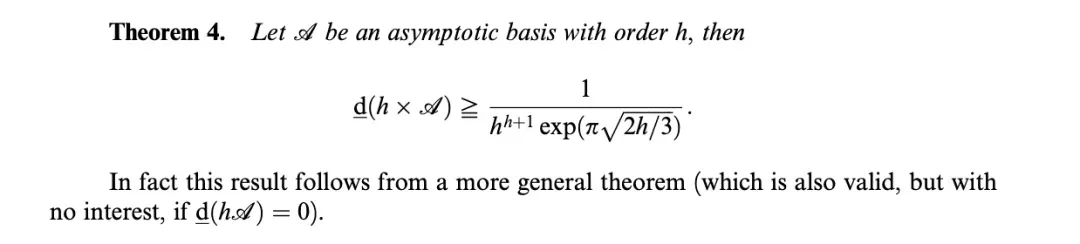
---
Significance
GPT‑5 Pro uncovered this forgotten proof using only a problem screenshot.
This demonstrates:
- AI as research augmentation — surfacing overlooked solutions.
- AI as “knowledge archaeologist” — rescuing valuable results from obscurity.
Creators and researchers can leverage integrative AI platforms such as AiToEarn官网 to:
- Generate content with AI assistance.
- Publish simultaneously across global platforms (Douyin, Kwai, WeChat, Bilibili, Rednote, Facebook, Instagram, LinkedIn, YouTube, Pinterest, X).
- Access monetization, analytics, and AI model rankings in one open‑source ecosystem.

---
About Paul Erdős
Paul Erdős (1913–1996) was one of the most prolific mathematicians of the 20th century.
Notable Achievements
- ~1,500 papers published, >500 co‑authors.
- Originator of the Erdős number metric.
- Major contributions to:
- Number theory
- Combinatorics & graph theory
- Probability theory
Early Life
- Born in Budapest, Hungary.
- At age 4: mental multi‑digit multiplication.
- At age 10: Self‑taught entire high‑school math curriculum.
Career & Style
- Earned doctorate at 21.
- Adopted a nomadic academic life — no permanent position, frequent collaborations.
- Preferred a “problem‑driven” research style.
Contributions
- Elementary proof with Selberg of the Prime Number Theorem.
- Founded study of Ramsey numbers; introduced probability methods into combinatorics.
Famous Conjectures
- Erdős discrepancy problem — proved partially by Terence Tao in 2015.
Erdős died in Warsaw in 1996, still active in research.
---
Modern AI in Mathematical Research
In 2024: British mathematician Thomas Bloom launched a site for studying Erdős problems.
Mathematician Paata Ivanisvili observed GPT‑5 Pro detecting flaws in published papers:

> “Five years ago, I spent several days finding a flaw in this paper; the author confirmed it. GPT‑5 Pro spotted the same flaw in 18 minutes, plus smaller ones.”


OpenAI president Greg Brockman reposted the observation.

Use case: Rapid logical consistency checks in academic literature.

---
Prompt Engineering Tips for Paper Analysis
- Add:
- > “Please deep read – no grep, no scan – 1,000 lines at a time”
- Perform a circularity audit.
---
Extending Erdős’s Spirit into the AI Era
Given Erdős’s collaborative and curiosity‑driven approach, modern AI can:
- Verify research results.
- Help solve long‑standing problems.
Platforms like AiToEarn官网 integrate:
- AI content generation
- Cross‑platform publishing
- Analytics & AI model ranking (AI模型排名)
These tools bring Erdős’s spirit of global collaboration into the digital age.

---
Official Erdős Problems website: https://www.erdosproblems.com/faq
---
References
- https://x.com/SebastienBubeck/status/1977181716457701775
- https://x.com/gdb/status/1977153596811804890
---
Erdős Problems is a curated portal for famous open challenges posed or inspired by Paul Erdős, spanning multiple mathematical fields. The FAQ offers historical context, guidance, and participation methods.
For researchers, creators, and educators, AI‑driven ecosystems like AiToEarn can transform problem discussions into monetizable educational or analytical content, distributed globally in multimedia formats.