What Makes OLTP Databases So Fast at Finding Data?
Preface
As a data engineer, I haven’t spent much time with OLTP databases like PostgreSQL.
I do know that, to improve in-database performance, there are specific techniques that optimize workloads the database typically supports.
- For OLAP systems, the goal is to prune as much data as possible.
- For OLTP systems, the goal is to find a record as quickly as possible.
But how exactly is that achieved?
In this article, we’ll explore one of the most widely used techniques in databases like PostgreSQL and MySQL: B-Trees.
We’ll begin with in-memory tree fundamentals, then build toward understanding how B-Trees work and why they’re so effective for indexing.
---
1. Tree Fundamentals
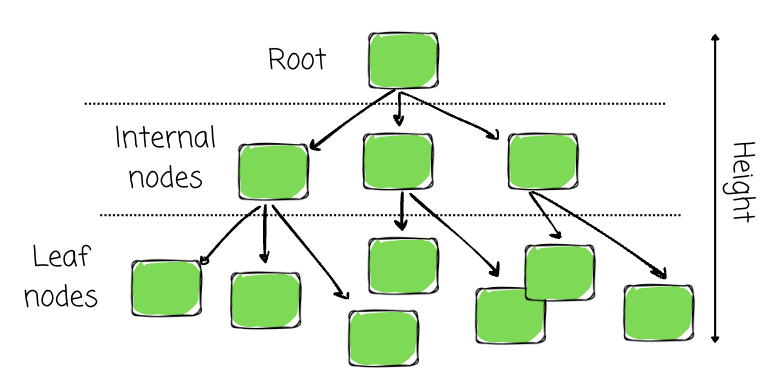
In computer science, trees model hierarchical structures, composed of linked nodes in various roles.
Key Definitions
- Node: Stores data and pointers to other nodes (leaf nodes hold no pointers).
- Root: The top node with no parent; all growth starts here.
- Leaf Node: Node with no children.
- Internal Node: A connector node with at least one child.
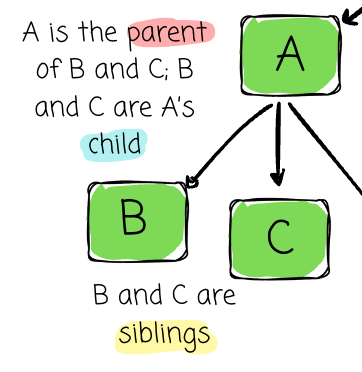
- Parent / Child / Sibling:
- If node A points to B and C, A is parent to both.
- B and C are children of A.
- Children of the same parent are siblings.
- Height: Distance from root to deepest leaf node.
- Subtree: A node and all its descendants considered independently.
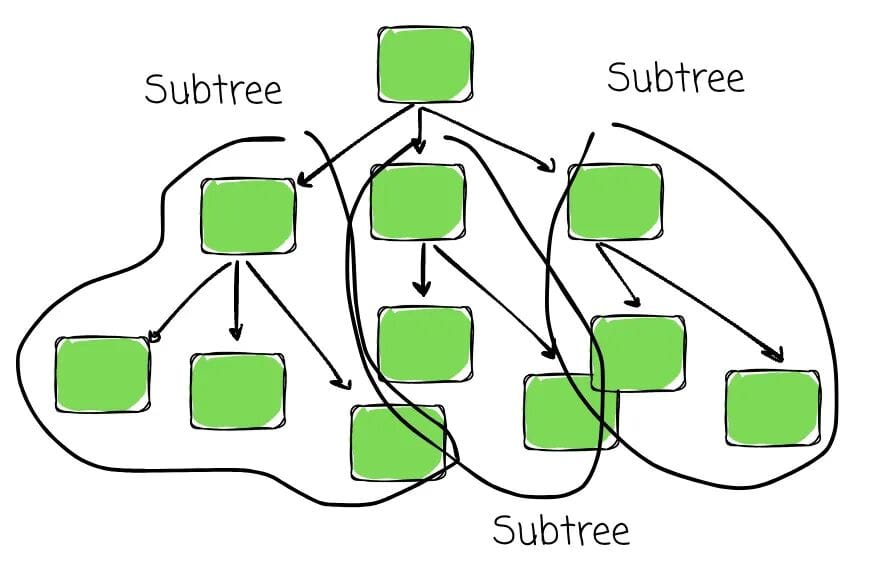
- Depth: Distance from the root to a given node (root has depth 0).
---
2. Binary Trees
Certain data structures suit specific use cases. One such structure is the Binary Search Tree (BST), built to enable binary search.
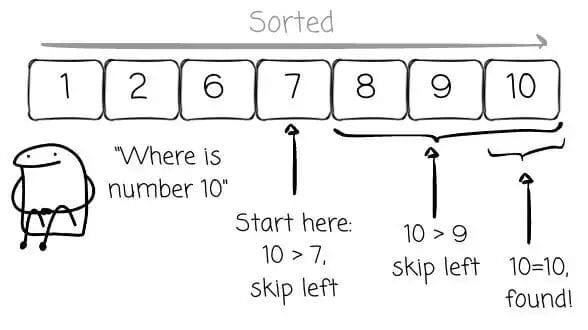
Binary search compares a target value with the middle element of a sorted array. Based on the result, half the search space is discarded, and the process repeats recursively until the target is found.
Example: array `1, 2, 6, 7, 8, 9, 10`
Searching for `10` starts with middle value `7`. Since `10` > `7`, we skip the entire left half.
BST Properties
- At most two children per node
- Left subtree values < node’s value
- Right subtree values > node’s value
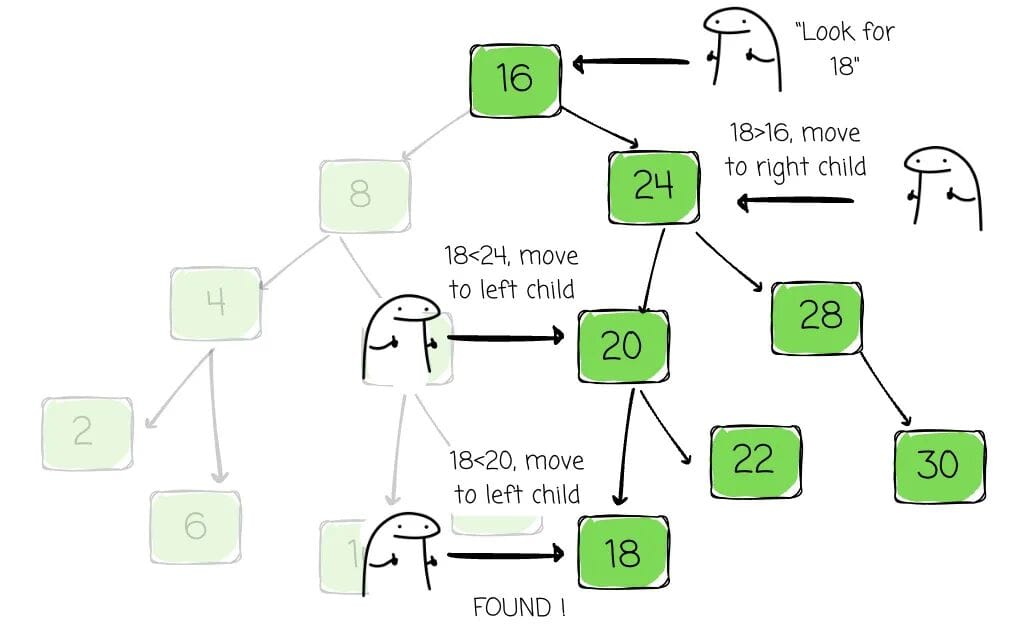
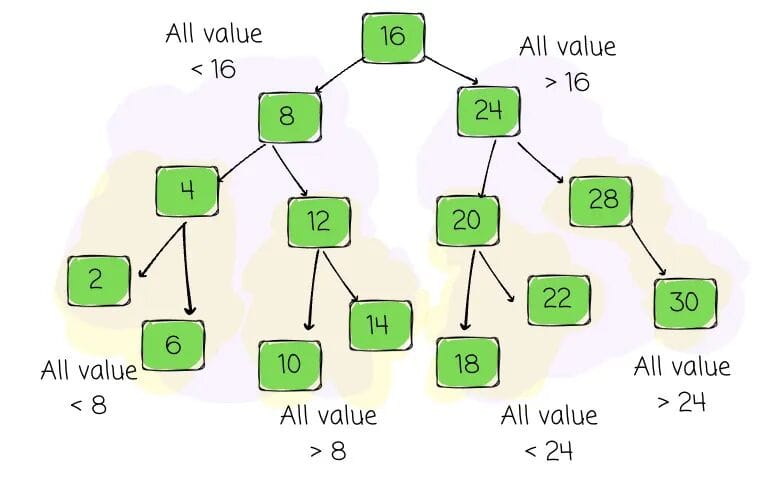
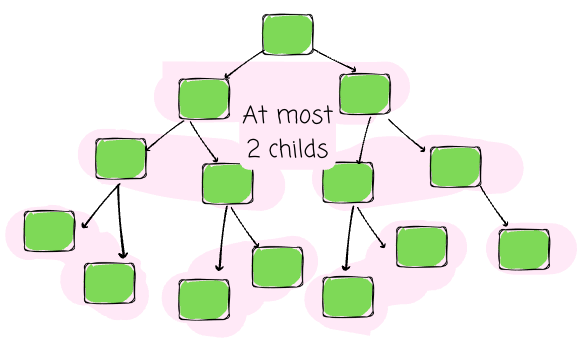
Searching starts at the root, comparing the target to node values, branching left or right until found.
Why not an array?
Sorted arrays make binary search possible for reads, but inserts/deletes require shifting elements — O(n) complexity.
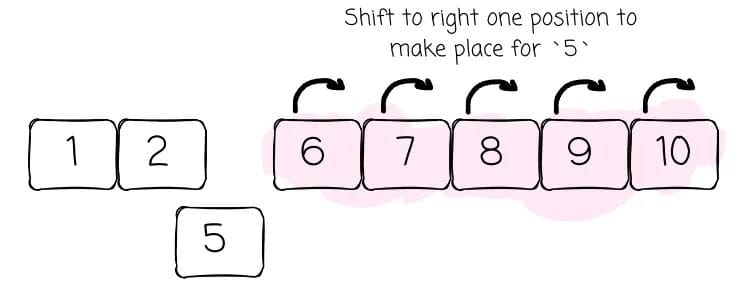
BSTs offer binary search efficiency for both reads and writes, though managing tree structure is more complex.
---
3. The Need for Balance
BST constraints alone don’t guarantee O(log n) performance.
A balanced tree — left and right subtrees of similar size — ensures optimal search and update speeds.
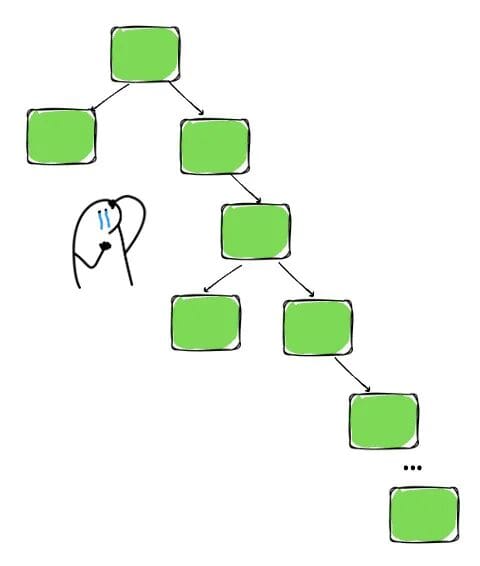
Imbalance leads to degraded performance akin to linear search.
Self-balancing variants include AVL trees and Red-Black trees (details beyond this scope).
---
4. Why Binary Trees Aren’t Ideal for Disk
BSTs excel in memory where random access is fast. On disk, random access is far slower:
- Memory access: nanoseconds
- HDD seek: milliseconds
- SSD access: microseconds
Databases must minimize disk I/O.
Since disks operate in fixed-size blocks (e.g., 4KB, 8KB), data structures should maximize the usefulness of each block read.
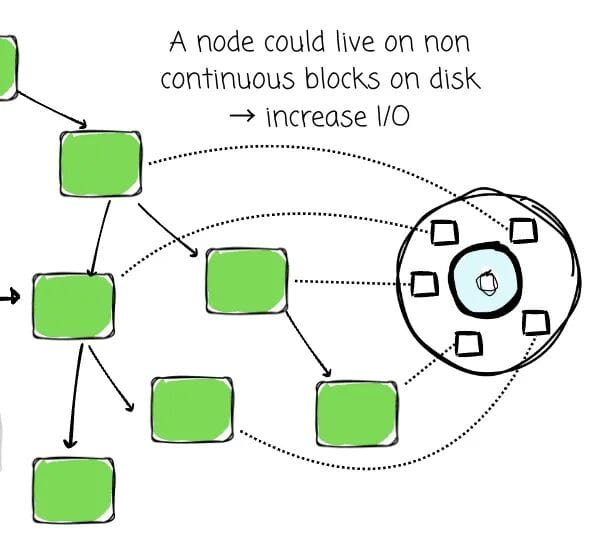
In BSTs, nodes are small (one value + two pointers), wasting space if stored one per disk block.
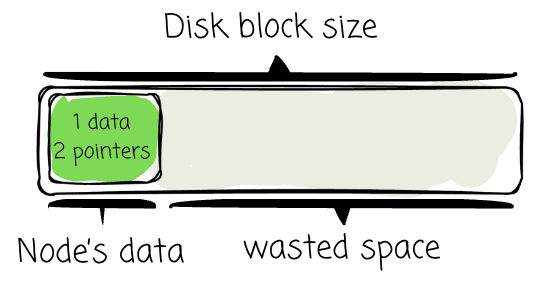
Traversal of a tall BST could require multiple disk reads per search — highly inefficient.
---
5. B-Trees
Databases needed something better: the B-Tree, introduced in the 1970s.
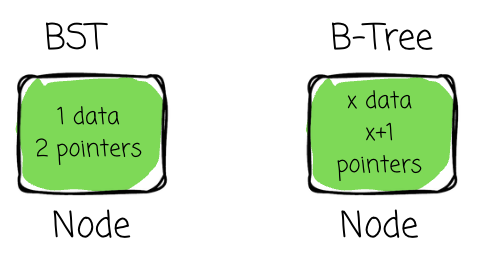
B-Trees:
- Self-balancing, generalizing BSTs
- Each node stores multiple keys and has multiple children
- Designed to align with disk block size for efficient page reads/writes
In PostgreSQL, for example, pages are 8KB.
---
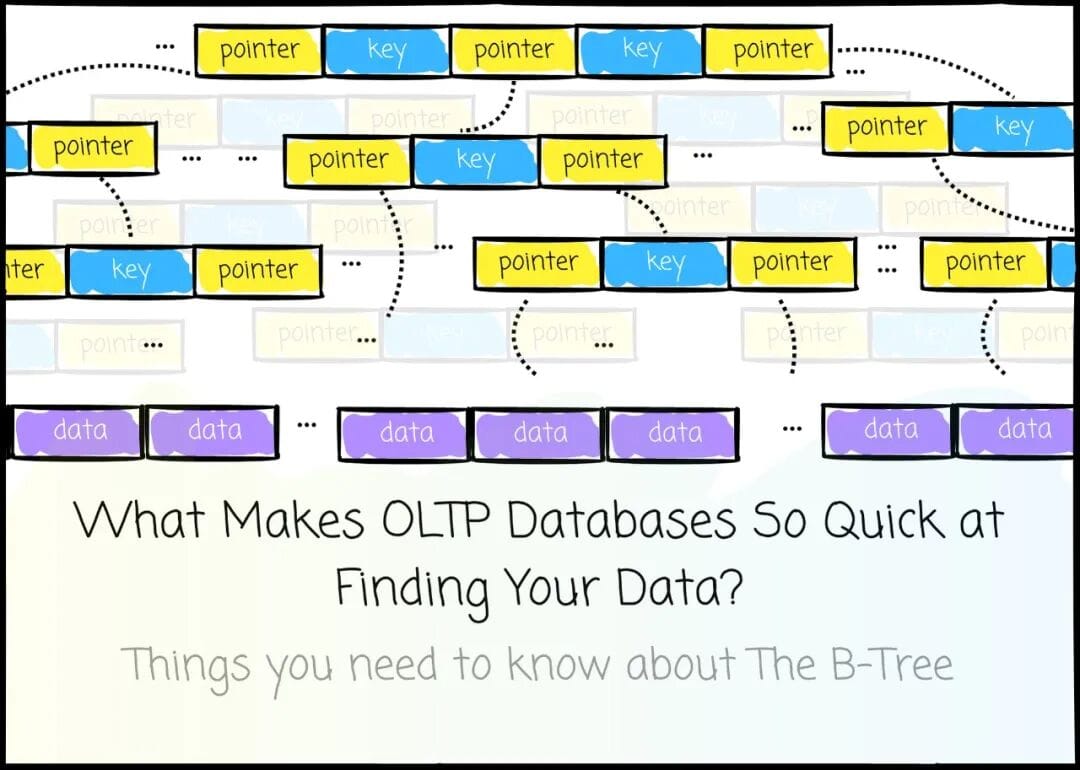
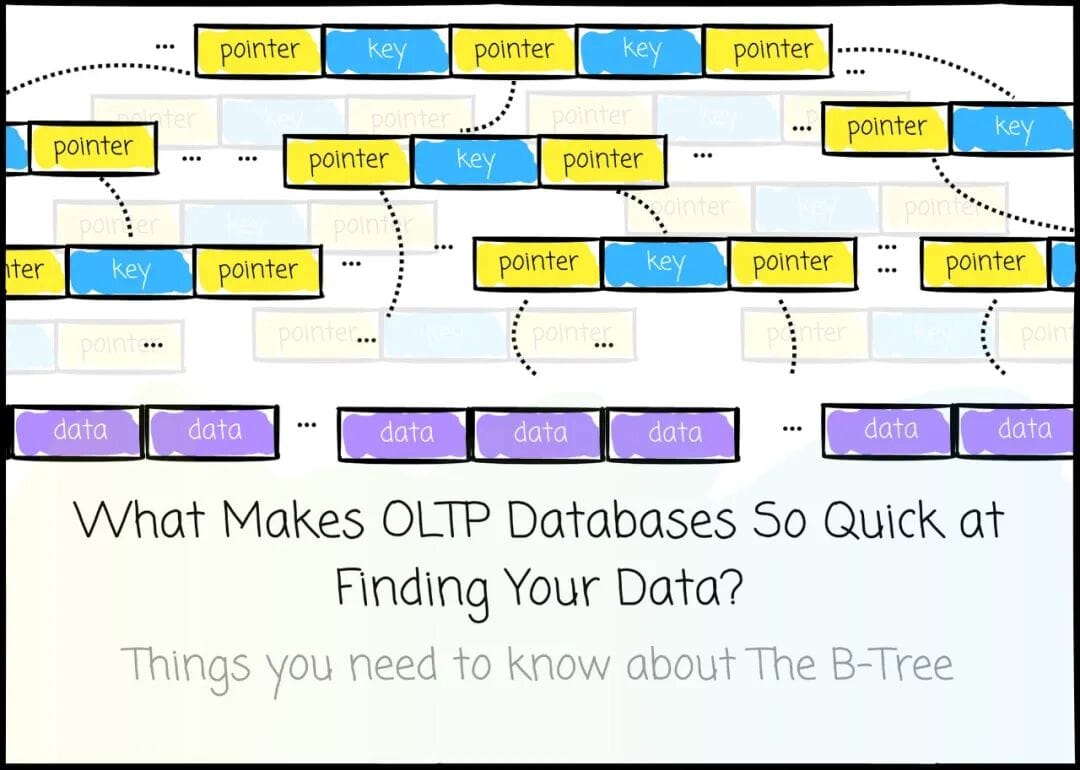
6. B+ Tree Anatomy
Most databases implement B+ Trees:
Only leaf nodes store data; internal nodes store indexed keys and pointers.
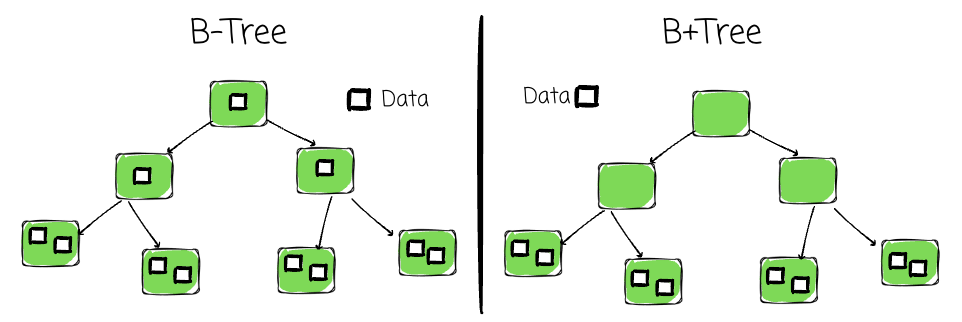
Key Concepts
- Order (M): Max number of child pointers per page
- Keys per node: Up to `N = M – 1`
- Min fill: At least `N/2` keys per node — avoids waste, maintains efficiency
- Root: Entry point for all operations
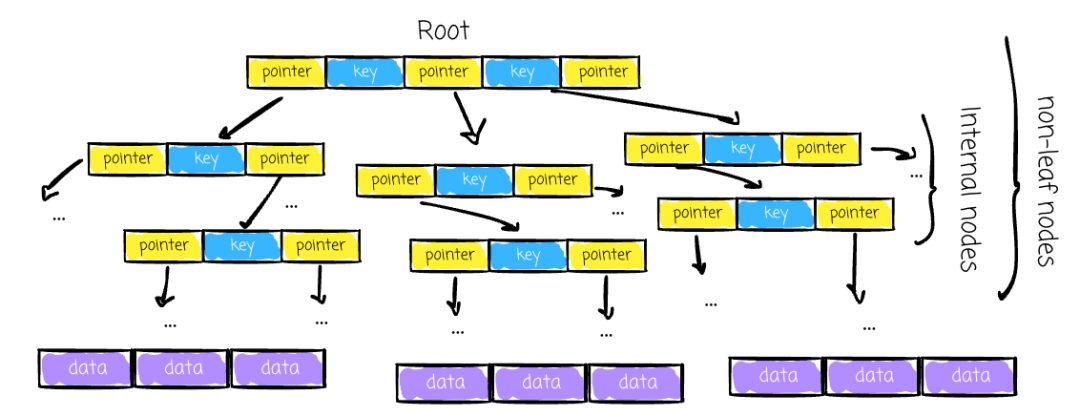
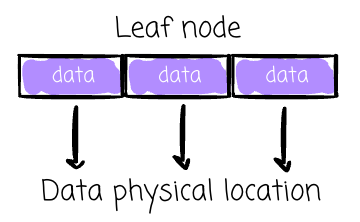
Non-leaf nodes store:

- Sorted keys
- Pointers to child nodes (`#pointers = #keys + 1`)
- Each pointer references keys in a defined range

Search Flow
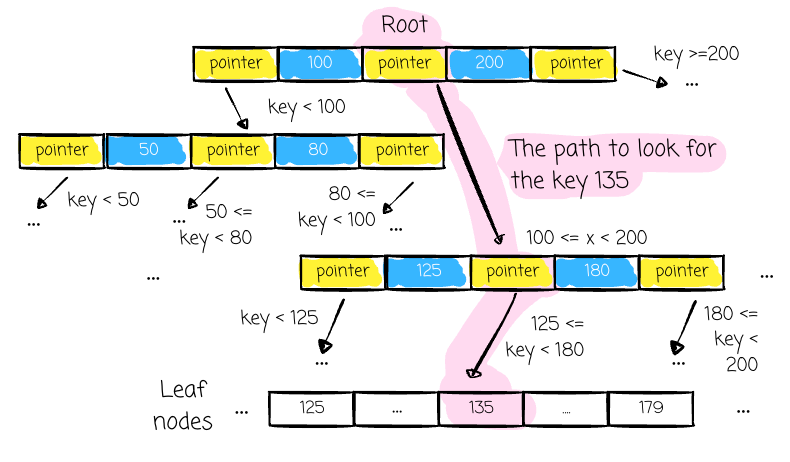
- Start at root
- Compare search key with node keys
- Follow appropriate pointer
- Repeat until reaching the correct leaf node
- Use stored pointer to access actual data
---
7. Handling Overflow
When inserting:
- If leaf has room → insert key
- If leaf is full → split node
Split Process
- Create new node
- Move the upper half of keys (`N/2+1` onward) into the new node
- Add new key & pointer to parent
Leaf overflow:
- Copy first key of new node to parent
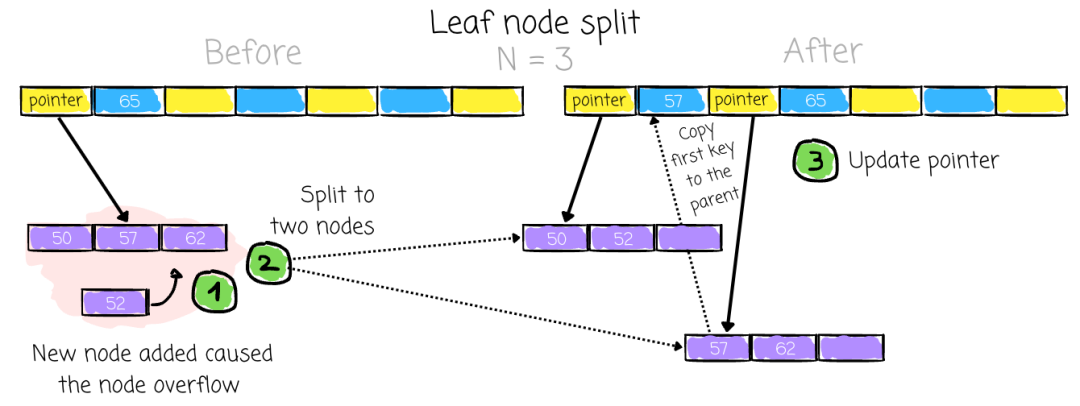
Non-leaf overflow:
- Move first key of new node to parent

Copying guides navigation; moving splits partitions without affecting data access.
---
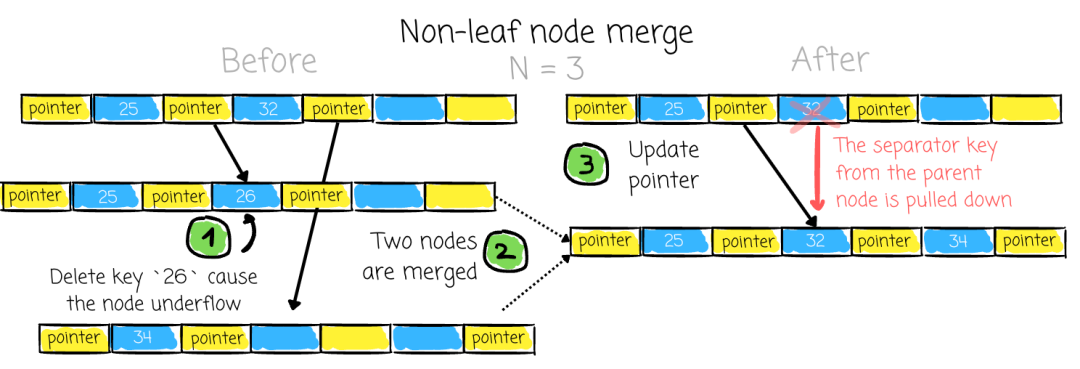
8. Handling Underflow
Underflow occurs when node keys drop below `N/2` (often after deletes).
Merge Strategy
- If siblings share a parent and can fit combined into one node → merge.
Leaf underflow:
- Merge keys and pointers
- Remove separating key from parent
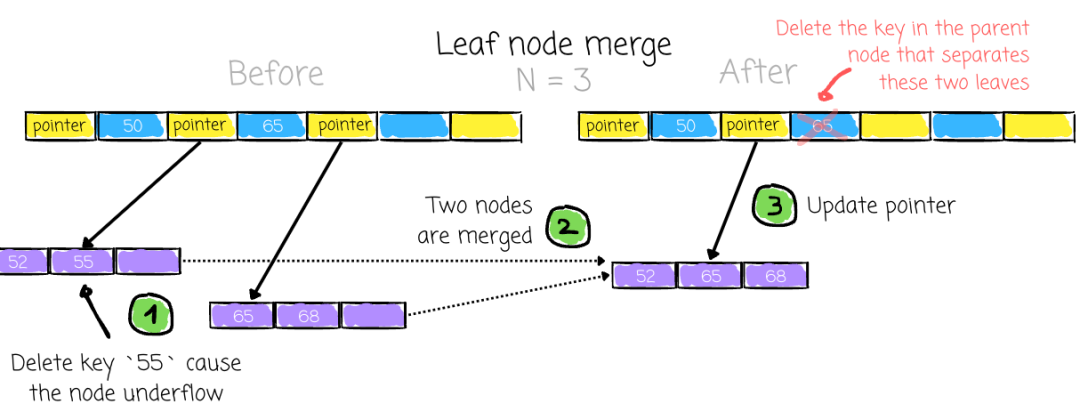
Non-leaf underflow:
- Pull down separating key from parent into merged node
- Merge all child pointers and keys
Merging may cascade up to the root.
---
9. Ensuring Reliability
Writes in B-Trees overwrite pages and may involve multiple pages (e.g., splits).
If an error occurs mid-operation, pages can be left inconsistent.
Solution: Write-Ahead Logging (WAL)
- Append all B-Tree updates to WAL before applying them
- On crash recovery, WAL ensures the tree returns to a consistent state
---
Conclusion
We reviewed:
- Tree basics & binary search property
- BST limitations on disk
- B+ Tree design for efficient disk use
- Overflow/underflow handling
- Reliability via WAL
B-Trees excel at reads; writes require careful structural maintenance.
In upcoming discussions, we’ll explore LSM trees, which focus on write-intensive workloads, common in OLAP systems.
---
References
- Martin Kleppmann — Designing Data-Intensive Applications (2017)
- O’Reilly Link
- Alex Petrov — Database Internals (2019)
- Amazon Link
- CS186 UC Berkeley — B+Tree Notes (2023)
- PDF Link
Source: Original article



